( إذا كان المثلثان ا ب ج و س ص ع متشابهان وكان ا ب = 10 س ص = 2 س ع = 6 فان ا ج = )
إذا كان المثلثان ا ب ج و س ص ع متشابهان وكان ا ب = 10 س ص = 2 س ع = 6 فان ا ج = ؟

مقدمة
المثلثات المتشابهة هي مثلثات لها نفس الشكل ولكنها قد تكون مختلفة الحجم. إذا كانت مثلثان متشابهين، فإن نسب أضلاعهما متساوية. وهذا يعني أنه إذا كان طول أحد الأضلاع في مثلث ما هو ضعف طول الضلع المقابل في مثلث آخر، فإن جميع الأضلاع الأخرى في المثلث الأول ستكون ضعف طول الأضلاع المقابلة في المثلث الآخر.

في هذه المقالة، سنستكشف مفهوم المثلثات المتشابهة ونحاول حل مسألة تتعلق بنسب أضلاع مثلثين متشابهين.
نسب أضلاع المثلثات المتشابهة

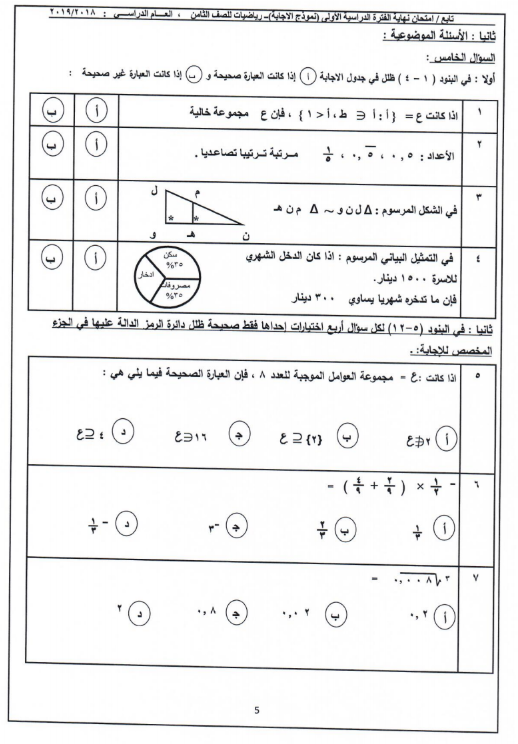
كما ذكرنا سابقًا، فإن نسب أضلاع المثلثات المتشابهة متساوية. وهذا يعني أنه إذا كان لدينا مثلثان متشابهان ا ب ج و س ص ع، فإن:
ا ب / س ص = ب ج / ص ع = ا ج / س ع
تطبيق على المسألة

في المسألة المعطاة، لدينا مثلثان متشابهان ا ب ج و س ص ع، حيث:
ا ب = 10
س ص = 2
س ع = 6
نريد إيجاد قيمة ا ج.
باستخدام نسبة أضلاع المثلثات المتشابهة، يمكننا إعداد المعادلة التالية:

ا ب / س ص = ا ج / س ع
بالتعويض بالقيم المعطاة، نحصل على:
10/2 = ا ج / 6
بإجراء العمليات الحسابية، نجد أن:
ا ج = 30
خاتمة
لذلك، فإن طول الضلع ا ج في المثلث ا ب ج هو 30. وهذا يوضح مفهوم المثلثات المتشابهة وكيف يمكن استخدامها لحل المسائل المتعلقة بنسب أضلاعها.