٢على٥، ٥على١٢، ١على٣
كسور متكافئة
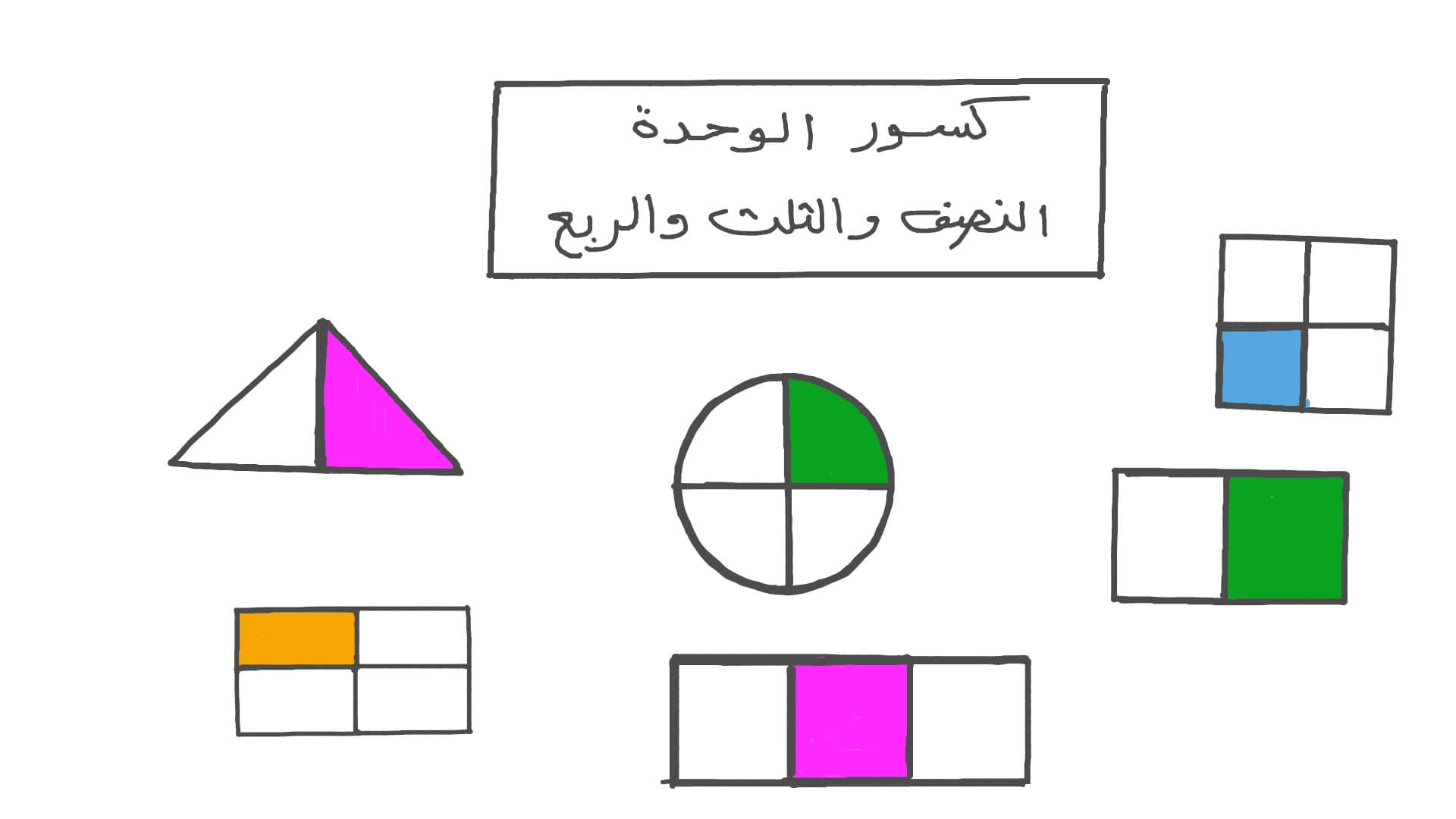
الكسور المتكافئة هي كسور لها نفس القيمة، على الرغم من أنها قد تبدو مختلفة. على سبيل المثال، ١/٢ و ٢/٤ هو متكافئان، لأن كلاهما يمثل نصف العدد الصحيح.
كيفية إيجاد كسور متكافئة
هناك طريقتان رئيسيتان لإيجاد كسور متكافئة:
الطريقة الأولى:


اضرب البسط والمقام في نفس العدد. على سبيل المثال، ١/٢ × ٢/٢ = ٢/٤، وهو متكافئ مع ١/٢.
الطريقة الثانية:
اقسم البسط والمقام على نفس العدد. على سبيل المثال، ٤/٨ ÷ ٢/٢ = ٢/٤، وهو متكافئ مع ١/٢.
أمثلة على الكسور المتكافئة
إليك بعض الأمثلة على الكسور المتكافئة:
١/٢ و ٢/٤
يمكن إيجاد هذه الكسور المتكافئة عن طريق ضرب البسط والمقام في ٢. ١/٢ × ٢/٢ = ٢/٤.
٥/١٢ و ١٠/٢٤
يمكن إيجاد هذه الكسور المتكافئة عن طريق ضرب البسط والمقام في ٢. ٥/١٢ × ٢/٢ = ١٠/٢٤.
١/٣ و ٢/٦
يمكن إيجاد هذه الكسور المتكافئة عن طريق ضرب البسط والمقام في ٢. ١/٣ × ٢/٢ = ٢/٦.
استخدامات الكسور المتكافئة
تستخدم الكسور المتكافئة في مجموعة متنوعة من التطبيقات، بما في ذلك:

العمليات الحسابية
يمكن استخدام الكسور المتكافئة لجعل العمليات الحسابية أسهل. على سبيل المثال، من الأسهل جمع ١/٣ و ١/٦ من جمع ١/٢ و ١/٤.
المقارنات
يمكن استخدام الكسور المتكافئة لمقارنة الكسور. على سبيل المثال، ١/٢ أكبر من ١/٣ لأن ١/٢ متكافئ مع ٣/٦ و ١/٣ متكافئ مع ٢/٦.
التناسب
يمكن استخدام الكسور المتكافئة لإعداد النسب. على سبيل المثال، إذا كانت النسبة بين أ والعدد ب هي ٢/٣، فإن النسبة بين ب والعدد أ هي ٣/٢.
أنواع الكسور المتكافئة
هناك نوعان رئيسيان من الكسور المتكافئة:
الكسور المتكافئة البسيطة

تُعرف الكسور المتكافئة البسيطة بأنها كسور ليس لها عوامل مشتركة بخلاف ١. على سبيل المثال، ١/٢ و ٢/٤ هو متكافئان بسيطان.
الكسور المتكافئة المركبة

تُعرف الكسور المتكافئة المركبة بأنها كسور لها عوامل مشتركة بخلاف ١. على سبيل المثال، ٤/٨ و ٦/١٢ هو متكافئان مركبان.

تحويل الكسور إلى أشكال متكافئة
يمكن تحويل الكسور إلى أشكال متكافئة باستخدام الطرق الموضحة أعلاه. من المهم ملاحظة أنه عند تحويل كسر إلى شكل متكافئ، لا تتغير قيمته.
الخاتمة
الكسور المتكافئة هي مفهوم أساسي في الرياضيات ولها تطبيقات عديدة في الحياة الواقعية. من خلال فهم الكسور المتكافئة، يمكن للأفراد إجراء عمليات حسابية، وإجراء مقارنات، وإعداد نسب، والمزيد.